Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 파이썬
- dropna
- computer vision
- 이미지처리
- dataframe
- 판다스
- 데이터프레임
- 머신러닝
- 비트와이즈
- NAN
- 지도학습
- scikit-learn
- tfidfvectorizer
- ML
- Deep learning
- 결측치
- Python
- 알파브렌딩
- KNeighborsClassifier
- 결측값
- NULL
- k-최근접 이웃 분류
- opencv
- mask detection
- 사이킷런
- sklearn
- Supervised learning
- pandas
- 이미지프로세싱
- index
Archives
- Today
- Total
Sun.El Data Analysis
[딥러닝] 퍼셉트론 및 게이트 개념 본문
728x90
1. 퍼셉트론 기초
1.1 개념
1.2 역할
1.3 생물학적 뉴런의 역할과 동작과정
1.4 퍼셉트론 동작과정
2. 단층 퍼셉트론(Single-Layer Perceptron)
2.1 개념
2.2 게이트(gate)
2.3 AND, NAND, OR 게이트 코드 구현
3. 다층 퍼셉트론(MultiLayer Perceptron, MLP)
1. 퍼셉트론 기초
1.1 개념
- 퍼셉트론(Perceptron)은 프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 제안한 초기 형태의 인공 신경망으로, 인공 신경망(Aritificial Neural Network, ANN)의 구성 요소(unit)로서 다수의 값을 입력받아 하나의 결과를 내보내는 알고리즘
- 퍼셉트론은 생물학적인 신경계(Neual Network)의 기본 단위인 신경세포(=뉴런)의 동작 과정을 통계학적으로 모델링한 알고리즘
- Perceptron은 perception과 neuron의 합성어이며 인공 뉴런이라고도 부름
1.2 역할
- 퍼셉트론은 이진 분류(Binary Classification) 모델을 학습하기 위한 지도학습(Supervised Learning) 기반의 알고리즘임
- 이진 분류는 아래 그림과 같이, 푸른색과 녹색 동그라미 2가지 클래스를 특정 기준 하에 구분함(예: 개 vs. 고양이)
- 두 클래스를 구분하는 기준은 붉은 직선이고, 이러한 기준(i.e., 여기선 직선)을 Decision Boundary라고 부름

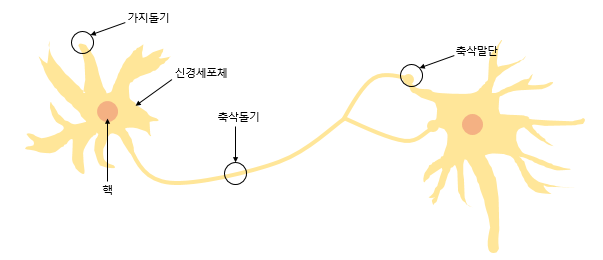
1.3 생물학적 뉴런의 역할과 동작과정
- 뉴런은 아래 그림과 같은 형태의 신경계를 구성하는 세포이며, 인접한 다른 뉴런과 다양한 신호(=자극)를 주고받으며 정보를 얻거나 저장하는 역할
- 뉴런은 가지돌기에서 신호를 받아들이고, 이 신호가 일정치(=임계값) 이상의 크기를 가지면 축삭돌기를 통해서 신호를 전달하며, 이러하 원리를 통해 출력 신호를 제어할 수 있음
1.4 퍼셉트론 동작과정
- 퍼셉트론은 뉴런이 다른 뉴런으로부터 신호를 입력받듯 다수의 값 x을 입력(뉴런 입력값)받고, 입력된 값마다 가중치(weight, w)를 곱합
- 가중치는 생물학 뉴런에서 뉴런 간 시냅스를 통한 결합의 세기와 같은 역할이며 가중치가 클수록 입력값이 중요하다는 것을 의미
- 입력값으로써 x외에도 편향(bias, b)은 딥러닝 모델 최적화의 중요 변수임
- 입력값과 가중치의 곱, 편향을 합산한 가중합을 퍼셉트론으로 전달함
- 가중합이 임계치(threshold, (Θ))를 넘으면 종착지에 있는 인공 뉴런은 출력 신호로서 1을 출력하고, 그렇지 않을 경우에는 0을 출력
- 이러한 가중합의 크기를 임계값과 비교하는 함수를 활성화 함수(Activation Function)라고 함

- 퍼셉트론은 활성화 함수로 계단 함수(Step Function)를 사용하고, 이는 가중합이 임계값(Θ)보다 클 경우 +1을 출력하고, 그렇지 않다면 −1을 출력

- 임계치를 좌변으로 넘기고 편향 b(bias)로 표현할 수도 있어 편향 b 또한 퍼셉트론의 입력으로 사용됨

- 보통 그림으로 표현할 때는 입력값이 1로 고정되고 편향 b가 곱해지는 변수로 표현함

2. 단층 퍼셉트론(Single-Layer Perceptron)
2.1 개념
- 값을 보내는 단계과 값을 받아서 출력하는 두 단계로만 이루어짐
- 각 단계를 보통 층(layer)이라고 하며, 입력층(input layer)과 출력층(output layer)으로 이루어져 있음

2.2 게이트(gate)
- 컴퓨터는 두 개의 값 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 게이트(gate)라고 부름
- 게이트 종류
- AND 게이트 : 두 개의 입력값 모두 1인 경우에만 출력값 y가 1이 나오는 구조
- NAND 게이트 : 두 개의 입력값이 모두 1인 경우에만 0이 나오는 구조
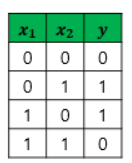
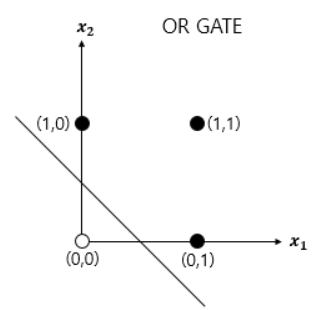
- OR 게이트 : 두 개의입력값이 모두 0인 경우에 출력값이 0이고 나머지 경우에는 모두 출력값이 1이 나오는 구조
- XOR 게이트 : 두 개가 서로 다른 값을 갖고 있을때에만 출력값이 1이 나오는 구조
| AND 게이트 | NAND 게이트 | OR 게이트 | XOR 게이트 |
 |
 |
 |
 |
 |
 |
 |
 |
- 단층 퍼셉트론을 이용하면 AND, NAND, OR 게이트는 구현가능하나, XOR 게이트는 구현할 수 없다는 한계가 존재
- 단층 퍼셉트론은 입력값에 따른 출력값을 구분짓는 직선을 1개밖에 그릴 수 없기 때문임
- XOR은 다음과 같은 논리기호가 적용되어야 하며, 2층 퍼셉트론이 필요함
2.3 AND, NAND, OR 게이트 코드 구현
- AND 게이트
[IN]
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7 #초기값인 가중치 1, 가중치 2 임계값 설정
tmp = w1 * x1 + w2 * x2
if tmp <= theta :
return 0
elif tmp > theta:
return 1
print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))[OUT]
0
0
0
1
- NAND 게이트
[IN]
def NAND(x1, x2): #NAND : AND의 출력을 뒤집은 것
x = np.array([x1,x2])
w = np.array([-0.5,-0.5]) #w1, w2에 -0.5 대입
b = 0.7
tmp = np.sum(w*x) + b #활성화 식
if tmp <= 0:
return 0
else:
return 1
print(NAND(0,0))
print(NAND(1,0))
print(NAND(0,1))
print(NAND(1,1))[OUT]
1
1
1
0
- OR 게이트
[IN]
def OR(x1, x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2 #편향에 -0.2
tmp = np.sum(w*x) + b #활성화 식
if tmp <= 0:
return 0
else:
return 1
print(OR(0,0))
print(OR(1,0))
print(OR(0,1))
print(OR(1,1))[OUT]
0
1
1
1
3. 다층 퍼셉트론(MultiLayer Perceptron, MLP)
- XOR 게이트는 기존의 AND, NAND, OR 게이트를 조합하면 만들 수 있음
- 다층 퍼셉트론과 단층 퍼셉트론의 차이는 단층 퍼셉트론은 입력층과 출력층만 존재하지만, 다층 퍼셉트론 입력층과 출력층 사이에 은닉층(hidden layer)을 추가되었다는 것에 차이가 있음


- 다층 퍼셉트론은 본래 은닉층이 1개 이상인 퍼셉트론을 지칭하고 중간에 수많은 은닉층을 더 추가할 수 있음

- 위와 같이 은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Network, DNN)이라고 함
- 심층 신경망은 다층 퍼셉트론만 이야기 하는 것이 아니라, 여러 변형된 다양한 신경망들도 은닉층이 2개 이상이 되면 심층 신경망이라고 함
※ 참고 : 게이트별 논리기호, 논리식, 진리

※ 참고사이트 : https://wikidocs.net/24958, https://heytech.tistory.com/332
'Deep Learning' 카테고리의 다른 글
| [openCV] 컬러 스페이스 (0) | 2023.08.22 |
|---|---|
| [openCV] ROI(Region Of Interest) (0) | 2023.08.22 |
| [openCV] Window management, Keyboard Event, Trackbar, Mouse event (0) | 2023.08.21 |
| [OpenCV] 도형 그리기 (0) | 2023.08.21 |
| [OpenCV] 이미지/동영상 읽기 및 저장 (0) | 2023.08.21 |